🪴 教学参考资料

Search

SearchSearch

三段论

Nov 24, 202417 min read

著名的 苏格拉底 三段论（实例）：

  • 所有的人都是要死的。
  • 苏格拉底 是 人。
  • → （所以） 苏格拉底 是 要 死的。

以上是一个三段论实例（有具体的素材），其 逻辑形式可以 抽象为：

  • 所有M都是P。
  • S 是 M。
  • → （所以） S 是 P。

如果 把 单称 当 全称 处理的话，应该是：

  • 所有 M 都是P。
  • 所有 S 都是 M。
  • → （所以） 所有 S 都是 P。

这是三段论 第一格的 AAA 式。

第一句 是 大前提。

第二句 是 小前提。

第三句 是综合 大、小 前提 推出的 结论。

三段论的逻辑结构

三段论是由三个直言命题组成的一种演绎推理 形式。

两个部分： 前提（大前提 + 小前提）、结论。

三个概念：三个直言命题中，有三个不同的概念。 这三个概念各重复2次，在三个命题中充当 主项、谓项。

这三个概念 在 三段论中被 称为 ：

S：小项。 结论的主项。也出现在 小前提中。 P：大项。 结论的谓项。也出现在 大前提中。 M：中项。 只在 前提中，在 大前提 和 小前提中 都出现。

对日常语言（非标准形式表达）中 S、M、P 的确定：

先看结论部分，命题主项是 S， 谓项是 P

然后看前提部分，包含 P 的命题是大前提，包含 S 的命题是小前提

在前提中重复两次、在结论中不出现的，是 M。

中项的作用

大项P 和 小项S，在前提中 不直接联系，只分别与 中项M联系。

通过中项的 “居中” 联系，得出 大项P 和 小项S 的关系，作为 结论命题。

这样的推理形式 是 间接推理。 它不是由一个命题直接推出另一个命题，而是由两个或以上的命题， 共同作为前提，推出结论。

中项M 在两个前提中重复出现，（在有效式中 能够）关联 小项 和 大项。

其关联作用可以通过Flash 图形 来理解。

以 第一格 各式的推导为例

式 与 格 简述

式

将标准三段论中 每一个命题的 类型（A、E、I、O ）写下，

就是一个3字母的式，例如 AAA 式、EAE 式、EIO 式等。

格

根据 标准三段论 的 大、小前提中，中项位置的不同，

将 标准三段论 分为 四个格：

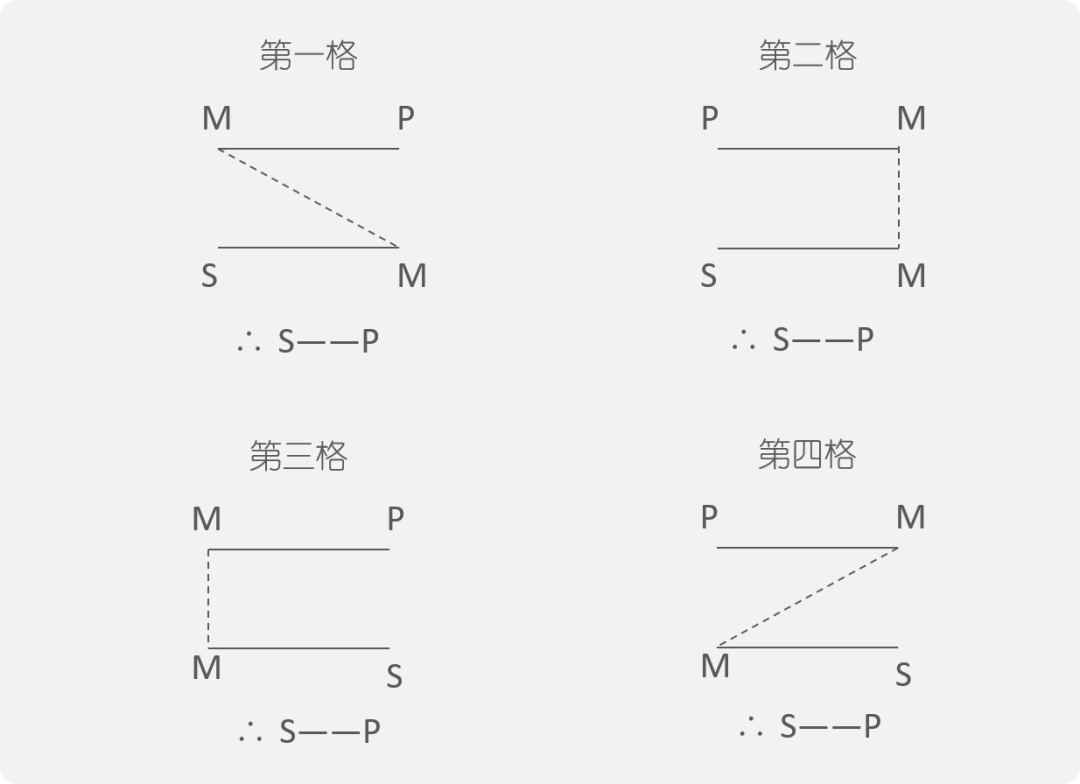
中项的具体位置：

格中项在大前提中的位置中项在小前提中的位置
第一格主项谓项
第二格谓项谓项
第三格主项主项
第四格谓项主项

把 大、小前提 中的 中项 相联，再把 四条线 放在一起，

布局类似 “业” 字的 上部。

格 + 式

要准确说明 一个三段论的式，需要加上 格。

可以 说 某格某式，也可以在式后加数字后缀。

例如： 第一格AAA式，或者 AAA-1

单纯排列的话，每一格的三段论有： 4×4×4=64个式， 四个格合计共有64×4=256 式。

但排除无效式，只有 24式（设定词项不能是空类） ，或 15 式（设定词项可以是空类）。

24式

第一格第二格第三格第四格
AAAAEEAAIAAI
AIIEAEAIIAEE
EAEEIOEAOEAO
EIOAOOEIOEIO
（AAI）（AEO）IAIIAI
（EAO）（EAO）OAO（AEO）

15 式

第一格第二格第三格第四格
AAAEAEIAIAEE
EAEAEEAIIIAI
AIIEIOOAOEIO
EIOAOOEIO
排除弱式排除弱式排除AAI、EAO排除弱式、AAI、EAO

三段论的逻辑规则

规则1

在一个三段论中，有且只能有三个不同的词项。

这里的“词项” 仅包括 主项、谓项。

直接使用 4个不同词语的 情况是很少见的，即使有 也 很容易 分辨。

需要注意的主要是 形式上是 三个词，但其实是四个概念的情况。

例如：

  • 鲁迅作品不是一天就能读完的。
  • 《从百草园到三味书屋》是鲁迅作品。
  • *所以《从百草园到三味书屋》不是一天就能读完的。

第一句的“鲁迅作品”是一个集合概念。（加“每一个”不通）

第二句的“鲁迅作品”是一个非集合概念。（加“之一”可以）

规则2

中项在前提中至少要周延一次。

一次都不周延不能必然推出结论。

  • 有些违法行为是犯罪行为。（MIP → MˣIPˣ）
  • 盗窃行为是违法行为。（SAM → SᵒAMˣ）
  • *所以，盗窃行为是犯罪行为。

分析：

① 有些违法行为是犯罪行为。 →中项M 和 大项P， 两个都不周延。 所以，本例可以理解为： 有些违法行为属于犯罪行为→ 有些违法行为是 犯罪行为 的一部分（子集）。 也可以换位： SIP→ PIS → 有些犯罪行为 是 违法行为 → 有些犯罪行为 是 违法行为 的一部分（子集）。

② 盗窃行为是违法行为。 →小项S 是周延的（这里的意思是 所有的 盗窃行为） 中项M，是不周延的， 所以，本例可以理解为： 盗窃行为 属于 违法行为 → 盗窃行为 是 违法行为 的一部分（子集）。

综合 ①、②， 则 有些犯罪行为 是 违法行为 的一部分（子集）。 假设为 a部分。 盗窃行为 是 违法行为 的一部分（子集）。 假设为 b部分。

a部分 和 b部分是什么关系？ 不能确定。

所以，在此三段论中， 盗窃行为（S） 和 犯罪行为(P) 的关系 不能 通过 违法行为(M) 关联起来 无法得出必然性结论。 推理形式无效。

勘误

也可以用图形来 理解。

再如：

  • 羊是动物。（PAMˣ）
  • 狗是动物。（SAMˣ）
  • *所以，狗是羊。（SAP）

PAM 中 M 不周延，所以无法确定 M 中与 P关联的部分（a）到底是哪部分， 同理，SAM 中 M 也不周延，所以也无法确定 M 中与 S关联的部分（b）到底是哪部分， a、b 都不定，所以无法 确定 a、b 之间的关系。

a、b 中 至少要有一个是 定的。

例如：AII-3

  • MᵒAP
  • MˣIS
  • SIP

虽然， MIS 中的 M 是不周延的，并不能确定 M 中与 S关联的部分（b）到底是哪部分， 但是 MAP 中的 M 是周延的，a 是全部的 M，是 P的一部分（子集）

由此，虽然不能 确定 b 到底是 M 的哪部分，但是 b 也能通过 M（这时等同于 a）与 a 关联起来。

即 因为 b 是 M 的一部分， M = a，所以 b 也是 a 的一部分，

而 a 包含于 P（是子集），所以 b 也是 P 的一部分，

（b 反过来说 也是 S的一部分），所以 S 的一部分 是 P的 一部分。

→ SIP

S、P 在前提中没有“见面”（直接关联），无法直接比对 两者的外延，

只能通过比对 P 与 M 关联的部分（a），以及 S 与 M 关联的部分（b）, 来间接地 分析 S、P 的关系。 如果 a、b 两个都是不定的，就无法分析了。

周延的外延好比一个整圆，形状大小是确定的。不周延的外延，形状不定，（代入到实例的话）可以画成一个同直径的扇形，也可以画成一个小一点的圆，也可能是一个相同大小的整圆，总之是不定的。

  • 泄密者是到会人员（PAM）
  • 甲是到会人员，（SAM，单称作全称）
  • *所以，甲是泄密者。（SAP，单称作全称）

规则3

在前提中不周延的词项，在结论中也不得周延。

参见 变形推理 中 的限制条件。

例如：

  • 诗人是人。（MAP）
  • 你不是诗人。（SEM，单称当全称）
  • *所以，你不是人。（SEP）

（也可以倒过来说，在结论中周延了，在前提中也必须周延）

规则4

两个否定前提推不出任何必然的结论。

只能 确定 a、b 都在 M 之外，a、b 具体是什么关系 无从分析。 S、P 的关系也就不能推定了。

当然 S、P 是可以有关系的，只是无法在 此推理形式中 必然地 推出。

例如：

  • MEP

  • MES

  • S ？P

  • 李田不是学生干部。

  • 李田不是三好学生。

  • 三好学生 ？ 学生干部

规则5

（ⅰ）如果有一个前提是否定的，则结论必然是否定的；

（ⅱ）如果结论是否定的，则必有一个前提是否定的。

⭐️以上五条规则，已足以将 有效的三段论 和 无效的三段论 区分开来。(陈波，逻辑学导论 5版，p.123)

如果大前提是否定的，则 a 在 M 之外，

依 规则4， 小前提必然是 肯定的， b 在 M 之内，

显然，b 在 a 之外。 S、P 的关系是个否定命题。

反之，如果小前提是否定的，则 b 在 M 之外，

依 规则4， 大前提必然是 肯定的，a 在 M 之内， 同理，显然也一样，b 在 a 之外。 S、P 的关系是个否定命题。

此时，a、b 以 M 为参照，总是一内一外。

例如：

  • 法律工作者不应知法犯法。（MEP）
  • 审判员是法律工作者。（SAM）
  • 所以，审判员不应知法犯法。（SEP）

本例（新编实用 p.89）读起来有些像 模态命题了 （使用了 “应”，“应该”）。

可以先 理解成 “法律工作者 不是 可以知法犯法的人。”

规则6

（ⅰ）如果两个前提都是肯定的，则结论必然是肯定的；

（ⅱ）如果结论是肯定的，则两个前提必然都是肯定的。

肯定的前提组合有 AA、II、AI、IA。

可试用 前 5个 规则 来分析，排除 所有 结论是 否定命题的 组合。

规则7

两个特称前提推不出任何必然的结论。

特称的前提组合有 II、OO、IO、OI。

可试用 前 5个 规则 来分析，排除 所有 组合 的有效性。

规则8

如果两个前提中有一个是特称，则结论也必然是特称。

（只）有一个是特称的前提组合有 AI、IA、AO、OA、EI、IE、EO、OE。

可试用 前 5个 规则 来分析， 只有 特称结论才是有效的。

导出规则的再推导： 规则8，可以用于 否定后件式的 推理。 如果 结论不是特称，那么 并非 两个前提有一个是特称。 即 并非 （大前提是 特称 或者 小前提 是 特称） 即 并非大前提是特称 并且 并非小前提是特称 即 大前提 是全称，并且小前提是全称

所以（对有效式来说）： 如果 结论不是特称，那么 两个前提都是全称。 如果 结论是全称，那么 两个前提都是全称。

规则8，肯定后件式的推理不成立：

  • 如果 结论是特称，那么 两个前提有一个是特称。

这个就不一定了，因为也可以使用弱式。

关于版本

通用规则（或称一般规则，对所有格都有效），各书的内容都基本相同。

只是 分类（不明确分类；分基本、导出两大类；把第一条拆出去作为前提，变成3类）

以及具体的表述（同一内容的用语、同类是否合并等） 有差异。

理解 并 记下来就行，先不要 太 纠结 版本。

补充及练习

三段论-辅助记忆材料

习题补充讲解-三段论

格

第一格

“经典格”（“典型格”）

结论包括所有类型，所以称“完善格”

司法中常用，所以称“审判格”

从一般情况、一般原理 出发， 对具体的事务进行判定。

对 未知的具体 ，进行判定

什么是什么

第二格

结论全是 否定

“区别格”

与第一格相同的地方是，

也是 对 未知的具体 ，进行判定

但 结论是否定的

什么不是什么

第三格

结论全是 特称 （大前提 四类都有） “反驳格”

有人说 什么都是什么，且不符合实际情况

可以用 第三格 来说明

有些 就不是

第四格

规则多，（实践）用处少

“冷门格”

可用来学习 做推理训练

通过图示来理解

在Flash中作图

可以提前全部画好

准备三个圆，其中一个带填充色 加文字标签

将圆 分别与 标签 组合

拖动、缩放、叠放 观察 S “圈”到的颜色 具体是什么情况 （即 S 与 P的 关系，P 带填充色，便于观察）

拖动、缩放、叠放，可以使用快捷键，快速选择对应的工具

在纸上作图

第一格

P 当“背景” （带填充色的圆） 圈出 M 再圈出 S

观察 S 的颜色

第二格

仍然是用P 当“背景”

但先圈出 M （只画圈） 再画P （带填充色） 再圈出 S（只画圈）

观察 S 的颜色

第三格

仍然是用P 当“背景”

先画出P （填充色） 再圈出 M （只画圈） 再圈出 S（只画圈）

观察 S 的颜色

AAI：M 在 S、P 的交叉部分中

第四格

仍然是用P 当“背景”

先圈出 M （只画圈） 再画出P （带填充色） 再圈出 S（只画圈）

观察 S 的颜色

AAI：P 在 M中，M 在 S中

以上是在纸上画图，可以有一定的顺序

Backlinks