(本节讨论 两个不同的概念 的外延的关系,只看 外延。)
从本节开始引入 符号 和 图示。
使用符号 S、P 、Q 等表示不同的概念。(具体用什么符号只是习惯问题,S、P 等比较常用,但用 A、B、C 也可以,只是代号。)
用圆形表示概念的外延,从而直观地考察概念间的关系。 除 字母 及直线外,没有别的标记,这样的图 称为 欧拉图。
相容关系
全同关系/同一关系
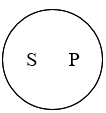
例如:
- 中国总人口最多的市 - 重庆市
- 1分钟 - 60秒
全同关系 与 同一概念 的区别:
- 前者是两个词、表达两个概念,这两个概念内涵不同(反映的本质属性不同),但外延刚好是一样的。这两个概念是全同关系/同一关系。
- 后者是两个词,所表达的概念,内涵相同、外延也相同,是同一个概念。两个词指向同一个概念。只有一个概念,就无所谓“关系“。
有的书没有严格区分这两种情况。李小克(7版,p.24)所举的例子“西红柿-番茄” 属于 同一概念。
真包含关系
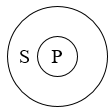
例如:
- 直辖市 - 重庆市
- 沿海省份 - 福建省
当 S 真包含 P 时,可以说 S、P 有 属种关系,S 是属概念,P是种概念。
何谓真包含?
真包含于关系
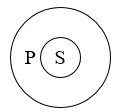 例如:
例如:
- 助词 - 虚词
- 名词 - 实词
当 S 真包含于 P 时,同样可以说 S、P 有 属种关系,不过这时 S 是种概念,P是属概念。
也有 严格对应顺序 说 种属关系的
交叉关系
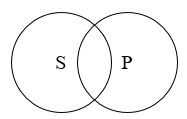
例如:
- 师大学生 - 本科生
- 适合学生使用的笔记本电脑 - 商务笔记本电脑
两个概念一般是从不同(但有关的)分类维度分出的
不相容关系/全异关系
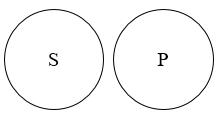
例如:
- 显示器 - 水笔
- 金属 - 非金属
- 黑色 - 白色
不相容关系/全异关系 可以再分出 矛盾关系 和 反对关系。
矛盾关系
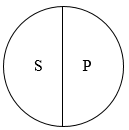
上例中的 金属 - 非金属 ,也是 矛盾关系。因为非此即彼。
即S、P 是全异关系,且S、P 同属一个 上级概念(属概念)。
S、P 的 外延之合等于上级概念(属概念)的外延。
上级概念(属概念)的外延中,除 S、P 外,没有别的。
反对关系
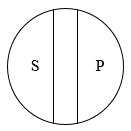
上例中的 黑色 - 白色 ,也是 反对关系。因为并非 非黑即白,并非 非此即彼。
即S、P 是全异关系,且S、P 同属一个 上级概念(属概念)。
S、P 的 外延之合小于上级概念(属概念)的外延。
上级概念(属概念)的外延中,除 S、P 外,还有别的。
李小克(7版,p.24) 将 全异关系 另立,把外延无重合,但既不是 矛盾关系,也不是 反对关系的 概念间的关系 称为 全异关系。
看法:如无特别的 或者 大的作用,一般还是不要改动长期延用术语的定义,以免混乱,得不偿失。 可以仍然 以 全异关系 为 矛盾关系、反对关系的上级概念,但说明一下存在 既不是 矛盾关系,也不是 反对关系的 全异关系。(另外,如果把上级概念的层级不断提高,几乎也都能归入 反对关系。)