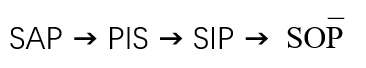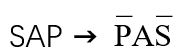回顾 对当关系 及基于此的直接推理:
要由一个 命题为真,去 推 另一(同素材)命题 也为真 时,
只有 差等关系 的 A → I, E → O 两个方向 可以 成立( 必然)。
以 A真 → I真 成立 为例,结合 周延性 ,可以说:
词项S,在前提 SAP命题 中作为主项, 是 周延的, 到了结论 SIP命题中,作为主项,是不周延的。 这样的变化是可以的。
即 (某个词项,在前提和结论中都出现,从前提到结论,其外延)缩小断定范围 是可以的,仍然能必然推出结论,推理是有效的。(演绎逻辑是 必然性推理)
- 所有金子都是闪光的。 → 这些金子(有的金子)是闪光的。
- 所有偶数都是可以被2整除的。 → 6、8、10(有的偶数) 是可以被2整除的。
但是,反过来不行,I真 不能 必然 推出 A真,
也即 扩大 断定范围 是不可以的(不必然能推出),推理形式是无效的。
在换位时,词项还是一样的词项,但位置的变化,会引起其周延性的改变,
这就 需要 注意以上问题,以保证推理的有效性。
复习: 直言命题 的 结构(各 词项)
换质法
同时也 换“谓”(谓项) (按 A、E、I、O 的顺序)
(可以 结合 Flash 图形 来观察)
1、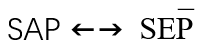
- 所有S 都是 P → 所有S 都不是 非P
- 所有的金属 都是 导电体 → 所有的金属 都不是 非导电体
- 所有的金子 都是 会闪光的 → 所有的金子 都不是 不会闪光的。
2、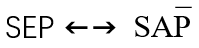
- 所有S 都不是 P → 所有S 都是 非P
- 所有的金属 都不是 非导电体 → 所有的金属 都是 导电体
- 所有的金子 都不是 不会闪光的。→ 所有的金子 都是 会闪光的
S、P等 只是代号。在 肯定命题中,P也可以是 负概念,同样,在 否定命题中,P也可以是 正概念。
3、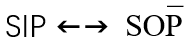
- 有的S是P → 有的S 不是 非P
- 有的学生 是 党员。 → 有的学生 不是 非党员。
4、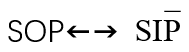
- 有的S不是P → 有的S是 非P
- 有的学生 不是 党员。 → 有的学生 是 非党员。
换位法
共3种,2个简单换位(直接对换位置),1个限制换位(要更换量项,限制所断定的范围)
(按 A、E、I、O 的顺序)
1、SAP → PIS (限制换位)
所有S都是P。 → 有的P是S。
所有金子都是闪光的。 → 有的闪光的是金子。
A命题不能简单换位,因为前提中 不周延的 P (肯定命题 谓项),在结论中会变成 周延的 (全称命题 主项)。
受 周延性 方面的限制,O命题 如果换位,则前提中不周延的 S(特称命题主项),在结论中会变成 周延的 (否定命题 谓项)。 代入实例,结论可能真,也可能假。不必然真,则为无效的(演绎)推理形式。
- 所有 汉字 都是 有读音的。 (SAP) → * 所有 有读音的 都是 汉字。(PAS)
- (全勤时本教室里)所有 在座的学生 都是 22级的学生。 (SAP)→ 所有 22级的学生 都是在座的学生。(PAS)
需要注意,不能以 某个具体结论 的 真假 来定 推理形式的 真假(有效与否)。前提真,则结论全都是真,(演绎)推理形式才是 有效的。
2、SEP → PES
所有S都不是P。 → 所有P都不是S。
所有唯物论者都不是有神论者。 → 所有有神论者都不是唯物论者。
3、SIP → PIS
有的S是P。 → 有的P是S。
有的学生是党员。 → 有的党员是学生。
O命题不能换位。
受 周延性 方面的限制,O命题 如果换位,则前提中不周延的 S(特称命题主项),在结论中会变成 周延的 (否定命题 谓项)。 代入实例,结论可能真,也可能假。不必然真,则为无效的(演绎)推理形式。
- 有的学生 不是 福建人。 ⇏ 有的福建人 不是 学生。
- 有的人 不是 网红。 —❌→ * 有的网红 不是人。
- 有的电脑 不是 笔记本电脑。 —❌→ * 有的笔记本电脑 不是 电脑。
同样需要注意,不能以 某个具体结论 的 真假 来定 推理形式的 真假(有效与否)。前提真,则结论全都是真,(演绎)推理形式才是 有效的。
换质位法
有的书,细分为 换质位法 和 换位质法,不过没有实质差异。
不管是 先换质 再换位,还是 先换位 再换质, 基本是 ABAB / BABA ……交替进行的。
先换质再换位:
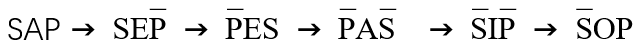


先换位再换质:
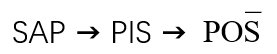
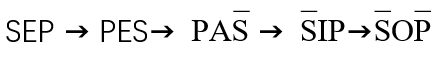
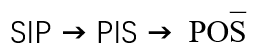
略有不同的 连续换位 的 情况:
以上的推导过程,出现了多个命题,有的书上 将之称为 换质换位综合推理(逻辑学辅导 第三版,赵泽宗,p.33)、换质法与换位法的综合应用(新编实用,p84)。
这(出现了多个命题)可能会给归类 上的 理解 带来一些麻烦:
这还是不是 直接推理 呢? 综合推理 跟 由两个或以上前提推出结论的 间接推理,又是什么关系?
在实际应用中,可以直接使用上面各式内部的 任意 两个 命题 (前后顺序要保持)。
例如: 所有 会员 都是 选举人。 → 所有 非选举人都是 非会员。(逻辑学导论,柯匹,15版,p.230)
换言之,是可以用来直接推出的。
所以仍然可以放在 直接推理 部分。
可以 把以上 各长式 看做是 直接推理(短式)的 “内部分解动作”(推导过程) 的说明。
空类问题
命题:
- 所有有机物是发展变化的,所以有些非有机物(即无机物)是不发展变化的。
其推理形式
来自:
)
其结论是假的。
那么 以上 推理形式 是否 是 有效的 呢?
这里涉及到一个 基本设定,即 S、P 可不可以是空概念(空类,不存在的,没有外延)。
如果不可以是空的,则 以上 推理形式 都有效。
而 如果可以是 空的,则 以上 推理形式 不都有效。
上面的命题中的 词项 “不发展变化的”,(在现代的哲学框架中)被认为是一个空类,
从而“动摇”了 基础,影响了 对 具体的推理形式 的 有效性的判定。
同样的情况也出现在 三段论中,如果 词项 不可以是 空的,有效的 三段论 有 24式,
如果 词项 可以是 空的,有效的 三段论 就只有 15式。