命题是反映事物状况的思维形式。(对事物性质有所断定的思维形式)
所谓事物状况,包括事物的性质、事物之间的关系等。比如某个事物具有或不具有某种性质, 或者与其他事物之间具有或不具有某种关系。
这种反映,来自(说话)人对事物状况的认识,通过与真实世界的对照,可知真假。
即命题是有真假之分的。
命题是通过句子来表达的。
有真假可言的句子才能表达命题。所以陈述句、反问句(无疑而问)才能表达命题。 (以上所说的命题是 形式逻辑的命题,其它逻辑分类的命题有所不同, 参见 形式逻辑-模态逻辑-辨证逻辑-区分)
命题是反映事物状况的思维形式。(在形式逻辑中)命题有真假。陈述句、反问句用于表达命题。
命题的结构
(或者说标准形式 直言命题(性质命题) 的结构)
将直言命题的内部结构分为 主项、谓项、联项、量项 四种词项。
在实际命题中,排列顺序为:
(量项)主项 + 联项 + 谓项
例如:
- 所有师大学生都是本科生。
- 有的师大学生是福建籍的。
- 所有师大学生都不是福州人。
- 有的师大学生不是硕士生。
结合例句,从汉语语法上看,作为命题的句子是 “主谓宾”式的(按句子成分分析法),
在句子中,主项 是 主语(的中心部分), 量项 是 主语的 (表示范围的)定语,联项 是谓语,谓项 是 宾语。
主项 与 主语 是差不多的,但 谓项 跟 谓语 不是一回事,谓语如果改写成“是……”的形式,则 谓项 是 宾语。
这样的分析,可能会不太好理解 谓项 的作用。
这里的谓语(谓语动词),是 “是”,如果转用 英语语法来看,“是”当系动词,“是”后面的部分就是表语(或 主语补足语)了,而表语 正是用来说明(谓)主语情况的。这也就是直言命题 谓项 的作用,即 说明 主项 的 性质。
再回到汉语语法, “主谓宾”式的句子,主语、宾语 通常是 由 体词性成分来充当的。即主语、宾语 一般是名词 或 代词。
综上,在标准形式 直言命题中:
- 主项 和 谓项,由名词 或 代词充当。
- 主项 是 命题所反映的事物,是被断定的对象。
- 谓项 用于说明主项的某种性质 。
- 量项 不是 “所有” 就是“有的”。量项 用来说明主项的 数量范围,或者说 用于说明 主项所表达的概念的外延,有多少被涉及了,是全部还是一部分。
- 联项 为 “是” 或 “不是” 。联项用于肯定或否定主项具有某种性质。
“都” 不属于 联项,它是总括主语的。 有些书在整理直言命题公式(标准形式)时,把“都”省去了。如果想要读得更通顺一些,加上也无妨。
可作为命题的日常语言的句子,也可以进一步改写为标准形式(N 是/不是 N),以方便理解和分析。
直言命题的分类
以S表示主项(Subject) ,P表示谓项(Predicate)
- A 表示全称肯定命题 (拉丁语Affrimo取第一个元音字母A)
- E 表示全称否定命题 (拉丁语Nego取第一个元音字母E)
- I 表示特称肯定命题 (拉丁语Affirmo取第二个元音字母I)
- O 表示特称否定命题 (在拉丁语Nego取第二个元音字母O)
英语的 affirmative、negative 能对上前三个
综合 量 (量项)和 质(联项) 的不同情况,直言命题一般可分为以下四种:
| 命题类型 | 名称 | 公式 | 标准形式 |
|---|---|---|---|
| 全称肯定命题 | A | SAP | 所有S都是P |
| 全称否定命题 | E | SEP | 所有S都不是P |
| 特称肯定命题 | I | SIP | 有的S是P |
| 特称否定命题 | O | SOP | 有的S不是P |
| 即 A命题、E命题、I命题、O命题。 |
全称、特称都是看主项的。
全称:全部、所有。
特称:不是全部、有的。
需要注意的概念:“有的”
术语 是 从 自然语言中 来的,但有特定的意思和用法,所表达的概念有相对严格的界定。
所以,一个术语,即使是与日常语言中的词“同形”且“近义”, 其概念 也是有所区别的。
“有的” 有多少?
逻辑学中的“有的”,是大于等于一个,不到全部,范围是从 1 到 比全部少1。
可以涵盖 “一个、两个、三个……”, “至少一个”,“极少数”,“少数”,“半数”,“多数”,“大多数”,“绝大多数”,“几乎全部”等等。
日常语言的“有的”没有这么大的范围,一般的语感可能到“半数”以下。
“有的是” 代表“有的不是”吗?
日常语言中,当我们说“有的是……”的时候,往往(虽然不绝对)意味着“有的不是……”。 这自然也就排除了“所有的都是……” 。
但是在逻辑学中,不是这样。
“有的S是P”(SIP),并不代表“有的S不是P”(SOP),也不否定“所有S都是P”。 即 SIP 为真,并不能推出 SOP 为真,也不能推出 SAP 为假。
推出SEP 为假 是可以的。
在日常语言中,“有的是……” 不(必然)代表 “有的不是……” 的情况:
一株是枣树,另一株……
一株是枣树,另一株是杨树
一株是枣树,另一株也是枣树
(另一株是枣树)真假不定
讲话卖关子:
一半人通过了,另一半人也通过了
以上 并非常用,但也是有的
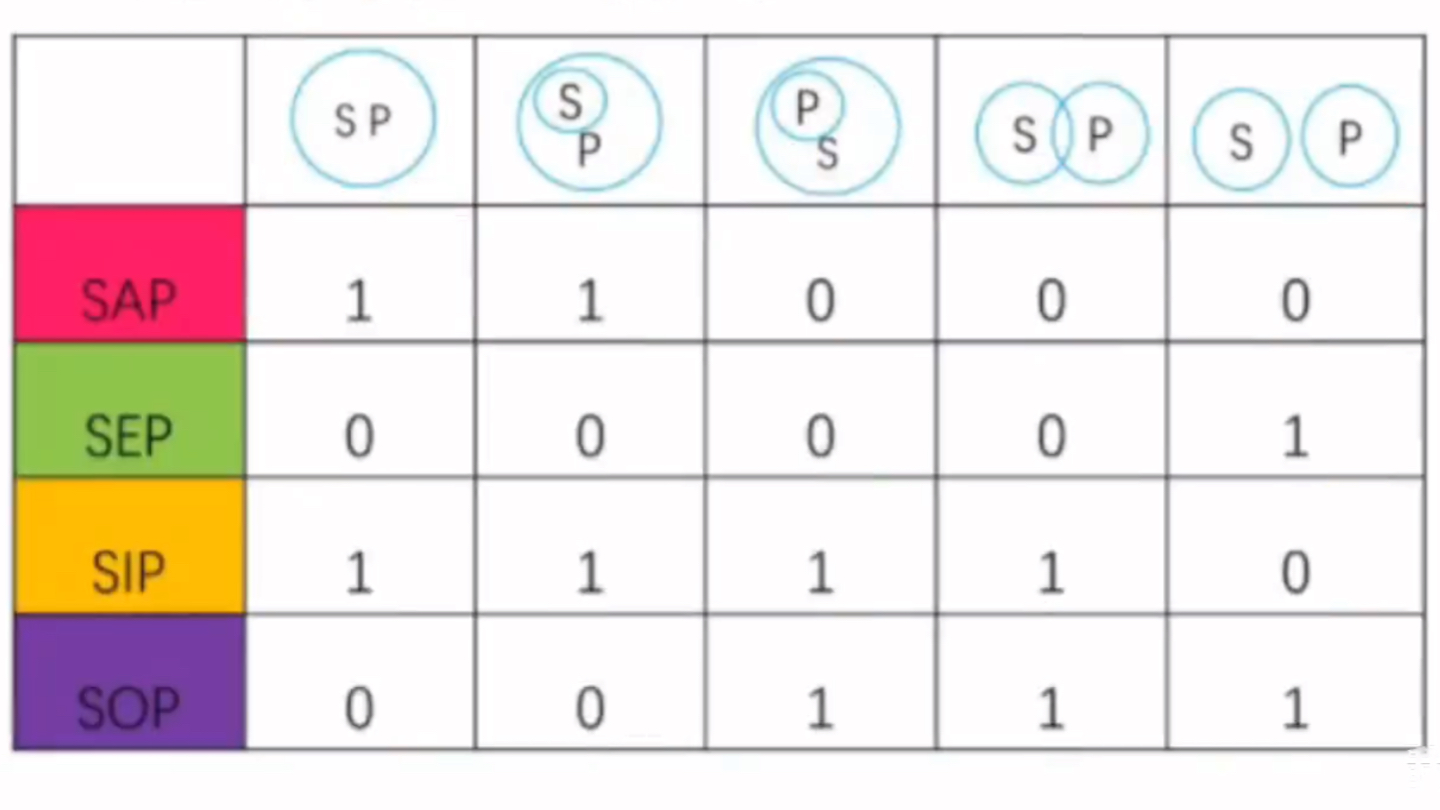
直言命题的外延关系图
需要注意的是,只有 SEP 是一对一的。
其它都是 一对二 或 一对多的。
与 很多人的日常表达习惯不同,形式逻辑中SIP真 并不必然代表 SOP也真。(如上所述,“有的是”并不必然表示“有的不是”。)
反之亦然。(“有的不是”并不必然表示“有的是”。)
所以SIP真,并不必然代表 S 与 P 是交叉关系。如下图,它们可能是除了“全异关系”之外的任何一种关系。
单称命题的处理
主项是单称(主项是单独概念,外延有且只有一个),外延数是1,
但 这个 1 和 特称 可以涵盖的1,不是一回事。
特称也可以是1,但这是2个、3个……中的1。
单称的1,是有且仅有一个的1。
1/1 = 100%,因此,这样的1,一般可以按全称处理。(例如讨论周延性时)
单称肯定命题 并入 全称肯定命题,单称否定命题 并入 全称否定命题。
有区别的时候再另外说明。例如在对当关系中,单称肯定命题 和 单称否定命题 就不是 反对关系,而是 矛盾关系。 单列时,公式为 SaP、SeP,用小写字母来区别。
主项、谓项的周延性
直言命题主谓项的周延性
Link to original
命题类型 主项 谓项 SAP 周延 不周延 SEP 周延 周延 SIP 不周延 不周延 SOP 不周延 周延