归纳推理
(一般认为)归纳推理 是 从特殊性前提 推出一般性结论 的 推理形式。
但并非完全如此。(参见 关于推理的种类)
基本形式
(a、b、c…… 都属于 P)
a…… b…… c…… ———— 所以,P……
P 是 a、b、c…… 所属的类。 a、b、c …… 可以是 具体的实例,也可以是类(此时P是更大的类)。
简单枚举法
即简单枚举归纳推理。
列举一定量的个例,且无反例,由此归纳推出对 全体的结论。
例如:
鸡天亮前叫三遍;
牵牛花破晓开放;
青蛙冬眠春晓;
大雁春去秋来;
人夜伏昼出。
……
————————————————
所以,生物体的活动都具有时间上的周期性规律
不能有反例。(或者说不能很好地处理反例)
例如,由“一只天鹅是白的,又一只天鹅是白的,……”简单枚举,推出“天鹅都是白的”,只要有一只“黑天鹅”就不成立了。
科学归纳法
即科学归纳推理。
以科学的方法, 通过对局部(部分)的观察、分析等,来归纳推出对 全体的结论。
例如:
种黄豆可以提高土壤肥沃程度,
种绿豆可以提高土壤肥沃程度,
种黑豆可以提高土壤肥沃程度,
种豌豆可以提高土壤肥沃程度,
种小豆可以提高土壤肥沃程度,
————————————————————————————————————————————————
所以,种豆类作物都可以提高土壤肥沃程度。
(再进一步详细分析,可知 豆类植物根部的根瘤菌与土壤肥力增高之间有因果关系)
科学在何处?
不仅有观察,还可以有实验。(不是仅能被动等待去观察,还可以主动创造条件去观察)
更广泛更合理的采样。
能处理反例。可以“化解”反例,例如通过分析说明这其实不构成反例,或者调整、细化研究的范围等。
(当然,“颠覆性”的确证反例另说)
尽管都是或然性推理,简单枚举法 与 科学归纳法 的信度可以有很大差异。
一般来说,后者高于前者。
可以 对比 “身边统计学” 与 严肃统计 的结论 来理解。
完全归纳法
穷尽了所有个例来归纳推出对全体的结论。
锐角三角形的内角和是180度。
直角三角形的内角和是180度。
钝角三角形的内角和是180度。
锐角三角形、直角三角形、钝角三角形是(按角分类的)全部的三角形。
(全部的三角形都可以按角分类)
——————————————————————————————
所以,三角形内角和为180度。
除此之外的都是 不完全归纳推理。
完全归纳的实现受到很多条件限制,自然条件、人力、物力、财力等。很多时候是无法开展的。有的是不必要的。
不完全归纳推理虽然尚未穷尽,但已有一定说服力(信度)。通过设计科学合理的方法,可以把信度提到很高的水平。
概率统计方法
(略) 通过统计方法推算出 某事在某条件下发生的概率。
多用于预测。与一般的确定性结论还有所区别。
具体的统计方法对结论也有很大影响。
穆勒五法
也称 排除归纳法 (陈波,第5版,p.198)
将明显无关的先行情况排除,从而在 其余的先行情况 和 被研究对象 之间确立因果关系。
先后出现的,不必然是 因果关系。
且先行情况可能有多个。
先行情况,和 所要研究的对象(某个后出现的情况)之间,是否存在因果联系?
具体是哪个? 需要使用一定的逻辑推理方法。
“先行情况”在有的书中也表述为“相关情况”。
求同法
例如:
敲锣发声时,如用手指触锣面,会感到锣面在振动;
用琴弓拉琴弦发声时,用纸条同发声的弦接触,纸条会被弦推动得跳动起来;
人说话时,如用手去摸咽喉,也会觉得它在振动。
——————————————————————————————
所以,声音是由于振动引起的。
可用公式表示为:
| 场合 | 先行情况 | 被研究的对象 |
|---|---|---|
| (1) | A、B、C | a |
| (2) | A、D、E | a |
| (3) | A、F、G | a |
| …… | ||
| 所以,A 与 a (可能)存在因果联系。 |
这里的“求同”是求“同现”(两者都出现)
再如:
(某人最近睡眠不好)
第一天晚上看了两小时书,喝了几杯浓茶,用热水泡脚,当晚没睡好。
第二天晚上看了两小时电视,抽了几根烟,用热水泡脚,当晚没睡好。
第三天晚上听了两小时音乐,喝了一杯咖啡,用热水泡脚,当晚没睡好。
——————————————————————————————
所以,没睡好是 ?引起的。
本例需要注意“似异实同”的情况。
求异法
可用公式表示为:
| 场合 | 先行情况 | 被研究的对象 |
|---|---|---|
| (1) | A、B、C | a |
| (2) | /、B、C | / |
| 所以,A 与 a (可能)存在因果联系。 |
类似 实验组 + 对照组
求异法中,被研究的对象 有变化之外,其它的要素都是一样的。
总体只有两组,两组的“先行情况”,除了 被研究的对象的“有、无”,是完全相同的。
常常要在人工控制下才能做到。
与 求同法、求同求异并用法 的对比
与 求同法 对比:
包含了被研究的对象的组,在 求异法 中只有一组( 场合(1))
而求同法有多组, 每一组都 包含了 被研究的对象,且每一组中除 被研究的对象固定外,
其它情况都是变化的。
与 求同求异并用法 对比:
求异法 的 场合(1) 可与 求同求异并用法 的 正面组 对比,
求异法 的 场合(2) 可与 求同求异并用法 的 反面组 对比,
差别都类似于 与 求同法的 对比。(1组 vs 多组, 多组中的其它情况都是变化的。)
求同求异并用法
可用公式表示为:
| 场合 | 先行情况 | 被研究的对象 |
|---|---|---|
| 正面(1) | A、B、C | a |
| 正面(2) | A、D、E | a |
| …… | ||
| 反面(1) | /、B、C | / |
| 反面(2) | /、D、E | / |
| …… | ||
| (综合比较 正、反的情况)所以,A 与 a (可能)存在因果联系。 |
求同求异并用法,有两次求同(一求“同现”,一求“同隐”),最后再 求异 得出结论。
与 求同法、求异法的相继应用 有什么区别?
求同求异并用法,在做 反面场合求同时,至少需要 2个反面例证
而求同法、求异法的相继应用,在到求异法时,只需要1个反面例证
共变法
可用公式表示为:
| 场合 | 先行情况 | 被研究的对象 |
|---|---|---|
| (1) | A1、B、C | a1 |
| (2) | A2、B、C | a2 |
| (3) | A3、B、C | a3 |
| …… | ||
| A1、A2、A3 是 A的不同变化。 a1、a2、a3 是 a的不同变化。 |
所以,A 与 a (可能)存在因果联系。(存在着有规律的共变)
剩余法
可用公式表示为:
A、B、C、D (复合先行情况) 是 a、b、c、d (被研究的复合结果)的原因。
B 是 b 的原因。
C 是 c 的原因。
D 是 d 的原因。
所以,(两边各自被剩下的)A 与 a (可能)存在因果联系。
关于推理分类的定义
《新编实用》p78 思维进程由一般到特殊的推理过程叫 演绎推理。
思维进程由特殊到一般的推理过程叫 归纳推理。
思维进程由特殊到特殊、一般到一般的推理过程叫 类比推理。
但是:
陈波,第5版,p191-193:
在演绎推理中:
(以假言推理的肯定前件式为例) p→q p 所以,q
命题变项 p、q 可以代入任意命题。如果我们代入一般性命题,则这个推理就是从一般到一般的推理:
如果谁热爱生命,谁就别浪费时间, 谁都热爱生命, 所以,谁也别浪费时间。
反之,我们代入个别性命题,该推理就是从个别到个别的推理:
如果马晓东想去美国念书,他至少必须获得赴美签证, 马晓东想去美国念书, 所以,他至少必须获得赴美签证。
从个别到特殊的演绎推理:
爱因斯坦是天才人物, 所以,有人是天才人物。
在归纳推理中:
从个别到个别的推理:
从我记事的第一天起,太阳从东方升起, 第二天,太阳从东方升起, 第三天,太阳从东方升起, …… 一直到今天,太阳从东方升起, ———— 所以,太阳明天仍从东方升起。
所以,定义并不能完全准确地概括
可以简单记住,总体上两者最根本的区别是:
一为必然性推理,一为 或然性推理(完全归纳推理除外)。
演绎推理 是 必然性推理,前提真,则结论必真。 归纳推理 是 或然性推理,前提真,结论很可能为真,但也有为假的可能。
归纳错误
无效的归纳推理:
以偏概全、轻率概括
样本不能太少
分布要有代表性
最后归纳出结论时也要 合乎逻辑和常理
(“直觉”或许常有“错觉”,但“常理”、“常识”不是可以轻易突破、“颠覆”的。)
无限线性外推
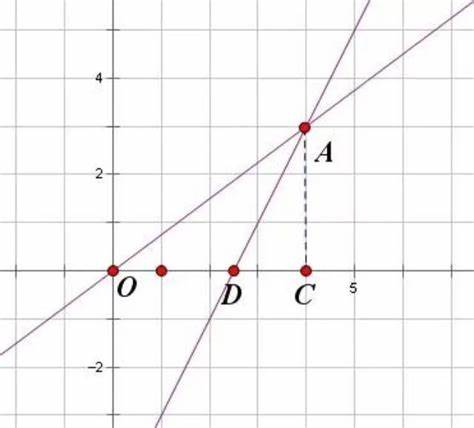
事物的发展不一定是线性的。
即使某一阶段看起来是线性的,也不代表可以持续以这样的趋势继续下去。
怎么看待归纳、统计的结论
了解其“采样”方法、数量、分布等 是否合理、充分。(前提)
分析其综合以上事例所进行的 归纳 是否 合理。(结论)
(对已证明有信度的统计)要相信总体概率, 但(面对具体“实例”)也可“保留几分”。(统计)
如何看待网上的信息?
信源。(原始出处是否可查、是否一致)
要素是否完整。(时间、地点、人物……)
逻辑是否自洽。(综合观察其长期以来的言论)
(注意以上其实就可以过滤很大部分的虚假信息, 之后才开始“动用”逻辑学知识进行分析。)
(《语言与逻辑》序言)
关于文学作品的典型形象
作品中的人物形象,通常是虚构的(“虚构” 跟 “虚假”还不一样)
也可以作为代表吗?
即使是虚构的,通常也有现实原型,且特质可能更为集中,所以也是某种意义上的归纳。
所以,典型形象是可以反映现实的。
问题在于是不是典型形象
是否能充分反映现实情况
是不是真的有代表性?真的相对全面、真实地反映了典型形象、典型事例?
这有时需要结合 作者背景、作品背景 来分析
我们语文课上曾背过的“枯燥”的作者生平,时代背景,这时就有作用了。
归纳与演绎的关系
演绎推理的前提 常是 归纳推理的结论。
构成归纳推理基础的 个别性(特殊性)前提,在其被获得时,也需要基于 演绎逻辑的 理论的指导。
归纳推理的结论 是 演绎推理的前提 的重要来源。
演绎推理的结论 是 归纳推理的(个别性)前提得以确立 的底层逻辑。