模态命题 是 包含模态词的 命题。
最常用的是 必然、可能(或然)这一对 模态词。
还有“必须-可以(允许)” 等
模态命题的对当方阵
模态命题的 必然肯定命题、必然否定命题、可能(或然)肯定命题、可能(或然)否定命题的真假制约关系:
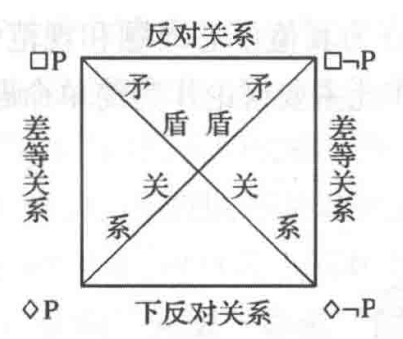
记忆方法: ☐ 正方形(看成立方体) 底面 放在地上是稳的,不动的,类似“必然”的意思。 ◇ 菱形(或者说 立方体的一条边),与地面的接触位置是一个点 或 一条线,是不稳的,类似“或然”(可能是 ,也可能不是)的意思。
如上图排列时,对当关系与 直言命题的 是一样的。
模态命题与实然命题的关系
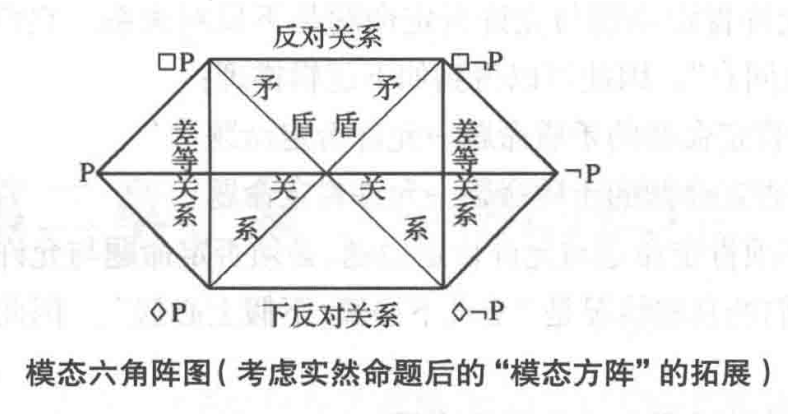
可通过 此方阵 理解 为什么 现实如何 不一定能定 模态命题的真假。
例如,早晨说 “ 可能 今天会下雨。”
如果到了中午,下了雨(p就为真了)
或者,过了晚上12点,没下过雨(p就为假了)
那么 同素材的 四类 模态命题的真假如何呢?
由上例也可以看出
“可能”的证明 以及 “必然”的 证伪,相对比较容易。
用一个成立的事例就可以证明 “可能”是,从而证伪“必然”不。
用一个不成立的事例就可以证明 “可能”不,从而证伪“必然”是。
但“必然”(是 或 不)的证明(完全的证明 或者 高度可信的证明) 是不容易的。