概念(词语) 在 命题(句子)中 充当 词项 时, 有周延或不周延之分, 这就是其周延性。
直言命题主谓项的周延性
| 命题类型 | 主项 | 谓项 |
|---|---|---|
| SAP | 周延 | 不周延 |
| SEP | 周延 | 周延 |
| SIP | 不周延 | 不周延 |
| SOP | 不周延 | 周延 |
在命题中,一个概念的全部外延都被明确涉及了,就称这个概念在这个命题中是周延的。
反之,就是 不周延 的。
可以把 周延或不周延 理解为 有多少外延进入了命题的判断中,是全部 还是 不是全部。
关于“周延”的表达
不同的书使用了不同的动词。
有的使用“陈述”:
【原文】词项的周延与否,是相对于某一个性质命题来说的,离开了性质命题,孤立的词项是没有周延性的。在一个性质命题中,如果对所使用词项的全部外延有所陈述,那么,这个词项在此性质命题中是周延的。如果只对所使用词项的部分外延有所陈述,那么,这个词项在此性质命题中就是不周延的。另外,我们说陈述了词项的全部或部分外延,是就性质命题的一般逻辑形式而言的,而不是特指某个具体的性质命题。 [@GuoJiaHong2010ZouJinLuo, p. 53]
有的使用“断定”(陈波,5版,p. 113;张志成,6版,p.42; 孟伟 唐明贵 p.45),有的使用“涉及”(李小克,7版, p.57)。
关于“涉及”:
“涉及”、“陈述”、“断定”,都可以理解为“说到”,
所谓 某个词项(在此命题中)周延,就是 该词项所有的 外延,
全部都 (在此命题中)被 “说”到了,“说”它是 或者 不是 什么。
所谓 某个词项(在此命题中)不周延,就是 该词项所有的 外延,
没有全部都 (在此命题中)被 “说”到了,“说”它是 或者 不是 什么 时,
不能必然涵盖所有外延。
可以说,
周延 所“涉及”、“陈述”、“断定” 的范围, 包含了 不周延 的范围。
至于代入实例,是 真包含、还是实际上相等的包含,就先不用考虑了。
总之,不周延(的外延) 是 周延(的外延) 的 子集。
主项的周延性
主项的周延性,根据 量项 来确定:
- 所有的汉字都有读音。 (SAP)
- 有的汉字有多个读音。 (SIP)
第一句的主项是全称,涉及了全部外延(全部外延都进入了判断),是周延的。
第二句的主项是特称,没有把全部外延都涉及到(不是全部外延都进入了判断),是不周延的。
非标准形式,可能没有直接写出量项,
例如:
- 人总是要有一点精神的。
- 福建人是好客的。
- 鲁迅作品不是一天就能读完的。
可以先根据逻辑知识、上下文、常识等来补出、改写,然后再确定。
第一句,可以变为:“所有人都是要有一点精神的。” (SAP)
第二句,可以变为:“大多数福建人是好客的。” (SIP)
因为按常识不能理解为“所有的/每一个福建人都是好客的。”
第三句,比较特别一些。
加“每一个”意思会变:“每一个鲁迅作品都不是一天就能读完的” (在这里真假都变了),可知主项“鲁迅作品”是集合概念,算单称,再并入全称,为SAP。
谓项的周延性
谓项的周延性,根据 联项 来确定:
联项 为 肯定,谓项 不周延。
联项 为 否定,谓项 周延。
谓项的周延、不周延 如何理解?
谓项的不周延
以全称肯定命题为例:
当我们说 “所有S都是P” 时,意思是 S(把外延当作集合看)中的每个元素,都与 P 中的一个元素对应。
但不能倒过来说,P中的每个元素 都与 S 中的一个元素 对应。可能 P中的某些元素 跟 S 中的任何元素都不对应。
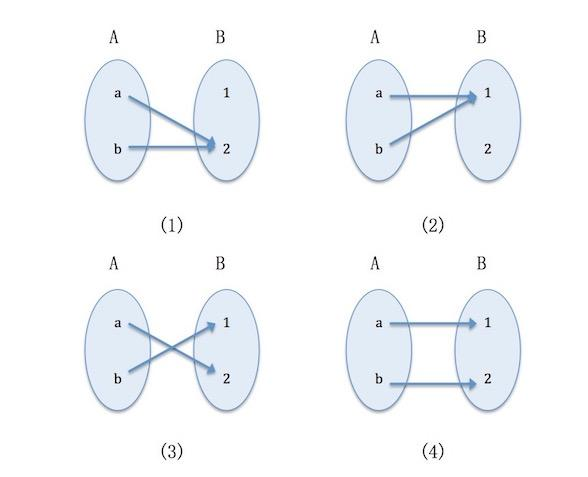
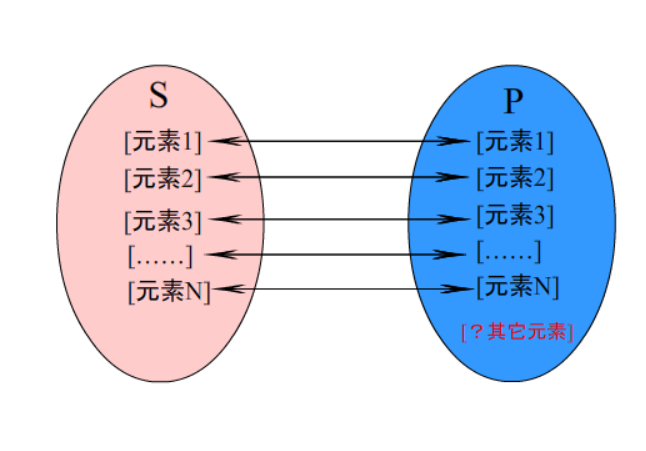
那么这些元素就没有被 “所有S都是P” 这个命题 涉及到。
即 “所有S都是P” 不能必然地推出 “所有P都是S” 。演绎推理 是 必然性推理,不能必然推出 就是 不成立。
也就是说,并不能 必然 确定 P 中的所有元素 都在这个命题中被 涉及到了。所以 P 是不周延的。
特别注意:在具体命题(有内容的)中不能将相关经验、知识直接代入,不能以现实中 两个 概念的(外延)关系来 代替基于逻辑规则的分析”
例:
- (全勤时)本教室里的学生都是23级学生。 (SAP)
我们当然知道,23级学生就是本教室里的学生,但不能用这个来代替基于逻辑规则的分析。
因为只要换一个说法:
- (全勤时)本教室里的学生都是本院学生。
就不能(把主项、谓项)倒过来说了。
逻辑规则是对普遍情况的抽象、概括,不必然的就不成立,SAP是推不出 PAS 的。
所以 SAP 中的P是不周延的,
现实的 归 现实,逻辑的 归 逻辑。
- 北京人都是中国人。
- 有的北京人不是工人。
- 所以,有的工人不是中国人。
结论这句话本身 是 真的。
但我们讨论的是推理的有效性。
把 作为 结论的 这句话,单独拿出来,看真假,是一回事。
由 两个前提 能不能推出 这个结论,那又是另一回事。
事实是一个层面,逻辑推理是另一个层面
两者可以有关联,但毕竟是不同层面的
不能以 结论本身 在 现实世界为真,来 证明 推理的有效性。
结论本身 在 现实世界为真,不能自动 说明 推理 就是 有效的。
遇到这类情况(自己知道 结论 是真,但 推理 形式已注明 无效),
如果不好理解,可以 把内容(素材)换一换,用同样的形式再推推看
例如:
- 北京人都是中国人。
- 有的北京人不是中国籍北大学生。
- 所以,有的中国籍北大学生不是中国人。
结论明显 为 假。
综合两个例子,可知,这个推理形式,(放入不同素材时),结论 可真可假,并非必然。
演绎逻辑 是 必然推理(前提真、结论必真),非必然 就是 无效 推理。
不要以 内容的 真假 ,代替 形式的真假(有效与否)
形式逻辑 的 形式,不是 “形式主义”的形式,
是 从 各种具体话语 中 归纳 出的、抽象的 形式
谓项的周延
理解了谓项的不周延,谓项的周延可能就比较容易理解了。
以全称否定命题为例:
当我们说 “所有S都不是P” 时,意思是 S(把外延当作集合看)中的每个元素,都不与 P 中的任何一个元素对应。(为什么加“任何”?)
说“任何”就已经 涉及到每个元素了,所以 P 的所有外延 都 被这个命题涉及到了,P是周延的。
这时是可以倒过来说的, “所有S都不是P” 可以必然地推出 “所有P都不是S” 。 即 SEP 可以推出 PES 。
周延性是演绎逻辑的“基石”
周延和不周延之间是什么关系?
(同一个词项),周延时被涉及的外延 和 不周延时被涉及的外延是什么关系?
全集 和 子集 的关系。 全集可以推子集,但是子集不能推全集。
演绎逻辑的基本推理原则可以怎么理解?
由 全集 推 子集 来实现“保真”。
可以简化地理解为“大推小”。
但是需要知道,在具体实例中,具体的外延间关系可能是“全集 和 真子集”,也可能是是“全集 和(实际上与之相等的)子集”。