(主要内容:复合命题、真值表、更多的逻辑符号)
概述
所谓“复合”,是说 复合命题 是由 简单命题 组合而成的,不同的逻辑组合方式构成了不同的复合命题类型。
简单命题 是 不包含 子/支命题的 命题,与 复合命题 相对,也称原子命题,即不可再分出命题的命题。(再分下去只有词项了)
直言命题 是 简单命题的一种。
复合命题的分类
复合命题 主要 包括 联言命题、选言命题、假言命题、负命题 这几大类。
命题 之所以也称 判断,就是对事物有所断定。
以上几类复合命题 所断定的内容,有所差别。
联言命题,仍是 对事物本身的断定,可以是对一个事物的两重 或 多重的断定,也可以是 对 两个或多个事物 同时 作断定。
知识,既是目的,也是手段。(苏霍姆林斯基)
北上广深是中国的特大城市。
选言命题,是对 所属支命题的 可能性 的断定。
校运会期间,研究生专业或者停课,或者不停课。(对未然的可能性的断定)
他或者是越南人,或者是泰国人。(对已然的可能性的断定)
假言命题,是对 所属支命题 之间的 条件关系 的断定。
如果明天下雨,那么比赛就要延期。
只有坚持科学练习,才能提高竞技水平。
负命题,是对 所属支命题(只有一个) 作否定性 的断定。
并非每个四川人都爱吃辣。
这个方法并非又好又快。(由紧缩复句构成的负命题)
教材所举的例子基本都是 由简单命题 直接组成 复合命题, 但是也可以层层嵌套。
联言命题
联言命题是断定两种或两种以上事物情况同时存在的复合命题。
北京是中国的政治中心,也是中国的经济中心。(一个事物的两重属性)
北京是中国的政治、经济、文化中心。(一个事物的三重属性)
华侨大学 和 暨南大学 是国侨办直属的大学。(两个事物的情况)
福建师大是省属的,厦门大学是部属的。(两个事物的情况)
逻辑结构
联言支 + 联结项 + 联言支……
联言命题中的 支命题 称 联言支。
联言支 是 简单命题吗?
联结项:使用符号为 ∧。∧ 使用术语读作“合取”,也可以用日常语言读作“并且”。 这是一个逻辑常项。
用于充当联结项的为 联结词,可以是符号,也可以是自然语言的词语。
通用度最高、最常用的 被称为 “典型联结词”。
联结词在日常语言中可以省略。
联言命题 可以理解为 是 确定性 的表述,没有“留选择空间”。
从语言学角度看,联言命题 可以属于 并列、顺承、递进、因果、转折等复句类型,但 在逻辑学中一般不考虑这些具体的关系。(李小克,7版,讨论了 转折 和 递进 的深层含义)
逻辑符号的使用
除了联结项 可以使用符号 ∧ 外,支命题也可以改用符号来表示,
以进一步提高形式化程度,方便演算、推理。
习惯上,从字母p开始,p q r s t u ……
在转换前,如果要使表达更清晰,还可以对 复合命题进行改写,拆分为 形式完整的若干 支命题。
例如:
北京是中国的政治中心,也是中国的经济中心。
可改写为: 北京是中国的政治中心,并且,北京是中国的经济中心。
北京是中国的政治中心。 命题p
北京是中国的经济中心。命题q
再加上 联结项:
p ∧ q
这样就将整个命题符号化了。
如果存在 命题的 嵌套,还需要使用 括号。
符号化的优点是 更简洁,更“聚焦”,推演更快。当然前提是 “翻译”要准确。
真值表的应用
联言命题的逻辑性质 即其 真假值。
真假值 简称 真值。
列表,将 各支命题 的真假值 、由其组成的 复合命题 的真假值,
对应排列,所得到的就是 真值表。
联言命题的真值表(逻辑性质)
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| 或 |
| p | q | p ∧ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
真 用 T(True)或 1 表示。
假 用 F(False)或 0 表示。
真值表 的列(从左到右),一般按命题字母顺序排列。
真值表 的行,p 命题 用 TTFF/ 1100 顺序(真真假假),q 命题 用 TFTF/ 1010 顺序(真假真假)。
联言命题的真值表(逻辑性质)为 3行假,1行真,(不算标题)第1行为真。
只有在 p、q 都真的情况下, p ∧ q (p 合取/并且 q)才为真。
后续真值表都使用 1、0 表示 真、假。
选言命题
选言命题是断定两种或两种以上事物情况中至少有一种存在的复合命题。
例如:
他或者是个律师或者是个教师。
(不能上网了)不是路由器的问题,就是电脑网卡的问题。
(以上也可以用 “要么……要么……”)
怎么理解 “至少有一种存在”(必有一真)?
在日常语言中,因为列举不全面,都不为真的情况也比比皆是。
例如:
A:他不是日本人,就是韩国人。
B:都不是。他是中国人。
所以,“至少有一种存在” 是说:
必须 “至少有一种存在” 才能使 选言命题 为真。
而不是说 必须 “至少有一种存在” 。 全是假的也可以,这就构成了一个 假的选言命题。
假的选言命题 也可以存在,也有它的用处。
逻辑结构
选言支 + 联结项 + 选言支……
选言命题中的 支命题 称 选言支。
联结项:∨,析取,或者。
合取、析取 符号的记忆: 从底向上看,“合二为一”的是 合取 ∧,“一分为二”的是 析取 ∨。
相容选言命题
前面说到 选言支 同假 的问题。
还有一个 选言支 同真 的问题。
根据 选言支 是否可以同真,可以将 选言命题 分为 相容选言命题 和 不相容选言命题。
在日常语言中,使用同样的联结词,有的句子是表示相容,有的句子是表示不相容。
完全相同的一句话,表示的是相容 还是 也相容,有时也可以有合理的不同理解。
比如 “要么……要么……” 中的 “选项”,是二选一,还是两个都可以,就是灵活的,要看具体语境,可能会有不同理解。
相容选言命题 为真时,可以有一个 或 一个以上的 选言支为真(包括 全真)。
相容选言命题真值表
| p | q | p ∨ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 相容选言命题的真值表(逻辑性质)为 3行真,1行假,(不算标题)第4行为假。 |
只有在 p、q 都假的情况下, p ∨ q (p 析取/或者 q)才为假。
两种命题的真值表刚好是相反的。
对比真值表可以帮助 比较 命题 间的差异。 便于进行 (同素材)复合命题间 的等值转换。
不相容选言命题
不相容选言命题 为真时,只可以有一个 选言支为真。
即 有且只有一个 选言支 为真时,不相容选言命题为真。
这一点可以用来推理。
同样的,不相容选言命题 中的 选言支 也可以全部为假,此时 不相容选言命题 为假。
不相容选言命题真值表
| p | q | p ⊙ q |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 不相容选言命题的真值表(逻辑性质)为 2行真,2行假,(不算标题)第2、3行为真。 |
只有在 p、q 只有一真的情况下, p ⊙ q (p 不相容析取 q)才为真。
假言命题
假言命题是断定两种事物情况之间存在某种条件关系的复合命题。
例如:
如果台风正面登陆,那么学校都要停课。
只有放在句中,多音字的读音才能确定。
(三段论)结论是否定的,当且仅当有一个前提是否定的。(倒装)
当且仅当有一个前提是否定的,则 结论是否定的。
“两种”是 概括的说法。
每“一种”的内部可以包含很多子项,但作为一个整体来谈论条件关系。
“两种” 事物之间 在 规模、数量上也未必是对等的。
所以 假言命题也可以用于描述 好几个事物(作为一个整体)与 另外的一个事物 或 好几个事物(作为一个整体)之间的条件关系。
例如:
多听、多说、多读、多写 才能学好 外语。
保证充分的练习、及时的复习 才能学好 发音、汉字、词汇、语法。
逻辑结构
假言支 + 联结项 + 假言支
假言命题中的 支命题 称 假言支。
只包含两个假言支,一为前件,一为后件。
前件 是 后件 的某种条件。
与 联言、选言命题不同,一个假言命题 只包含 前件 和 后件 两项支命题,不能“横向”扩展增加支命题数量。
但可以 “纵向”扩展,支命题可以是复杂命题。
充分条件假言命题
联结项:
→,蕴涵,如果……那么
充分条件假言命题真值表
| p | q | p → q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 充分条件假言命题的真值表(逻辑性质)为 3行真,1行假,(不算标题)第2行 为假。 |
只有在 前件真,后件却为假的情况下,p→q才为假(条件关系不成立)。
必要条件假言命题
联结项:
←,逆蕴涵(反蕴涵),只有……才
“只要……就……”一般算哪一类 假言命题?
必要条件假言命题真值表
| p | q | p ← q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 必要条件假言命题的真值表(逻辑性质)为 3行真,1行假,(不算标题)第3行 为假。 |
只有在 前件假,后件却为真的情况下,p←q 才为假(条件关系不成立)。
充分必要条件假言命题
联结项:
↔,等值,当且仅当,等值于
充分必要条件假言命题真值表
| p | q | p ↔ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 充分必要条件假言命题的真值表(逻辑性质)为 2行真,2行假,(不算标题)第2、3行(中间两行) 为假。 |
在 前件真,后件却为假,以及 前件假,后件却为真 的情况下,p↔q 为假(条件关系不成立)。
即 兼有 充分条件假言命题 和 必要条件假言命题 为假的情况。
其它
当我们说 一个 命题是 充分条件 或 必要条件 命题时,是同时排除了其为 必要条件 或 充分条件 命题的可能吗?
要明确分类的话,实际应用中 可以有 充分不必要、必要不充分、充分且必要、既不充分也不必要。
具体的(代入实际内容的) 联言命题、选言命题、假言命题,对其支命题的真假,以及整个复合命题的真假的判定,都需要 有相关背景知识;而不同的人掌握、理解的知识存在差异,因此同一个命题也会存在不同的解读。
负命题
联结项:
﹁,并非、非,……假
与 否定命题的 区别
“都不是” 是一个否定命题,是对 主项(主语)的(某个属性的)否定。
“不都是” 是一个负命题,即“并非都是”,是对 肯定命题 “都是” 的否定。
“都不是” 对应的 负命题应该是什么?(用对当关系 推)
复合命题的等值转换
同素材 的复合命题之间可以进行 等值转换。 负命题 和 原命题 自然也是 同素材的。
所谓 等值,是指 整个逻辑表达式的 同真同假。
要把 等值转换 理解清楚,最重要的方法 可能是 用好真值表。
同样的,要判定两个同素材的复合命题不等值,用真值表也较直观。
复合命题的负命题的等值式
复合命题的负命题,具体表示怎样的逻辑关系,转成等值式会更清晰。
方法是,先设定 一个复合命题为真,然后查看真值表,
找到为假的行,写出其逻辑表达式,即为 其负命题的等值式。
在实际生活中,对一个复杂命题,只是作简单的肯定回答 或 否定回答,都可以引起误解,或被刻意误用。
有时是有必要完整地“展开”的。
联言命题的负命题的等值式
联言命题的真值表为:
| p | q | p ∧ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 先设定复合命题 p ∧ q 为真,则(为真的) p ∧ q 对应第1行, |
那么其负命题 ﹁(p ∧ q)则对应 第2、3、4行,
观察这3行可知, (p ∧ q) 为假时,或者 p、q 一真一假,或者 p、q都为假,
也即 p、q 中至少一个为假。
因此,可以将这3行的情况 归纳为 一个选言命题。
同样的,设定命题p、q为真,则 p、q 为假就写为 ﹁p、﹁q。
所以,复合命题 p ∧ q 的负命题就写为:
﹁p ∨ ﹁q
等值关系式写为:
﹁(p ∧ q) ↔ (﹁p ∨ ﹁q)
需要更清楚地标出一个复合命题(以及一个作为负命题的支命题的复合命题)的起始位置时,可以加上括号
相容选言命题的负命题的等值式
相容选言命题真值表为:
| p | q | p ∨ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 先设定复合命题 p ∨ q 为真,则(为真的) p ∨ q 对应第1-3行, |
那么其负命题 ﹁(p ∨ q)则对应 第4行,
观察第4行可知, (p ∨ q) 为假时, p、q都为假,
因此,可以将第4行的情况 归纳为 一个联言命题。
同样的,设定命题p、q为真,则 p、q 为假就写为 ﹁p、﹁q。
所以,复合命题 p ∨ q 的负命题就写为:
﹁p ∧ ﹁q
等值关系式写为:
﹁(p ∨ q) ↔ (﹁p ∧ ﹁q)
不相容选言命题的负命题的等值式
不相容选言命题真值表
| p | q | p ⊙ q |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 不相容选言命题的真值表(逻辑性质)为 2行真,2行假,(不算标题)第2、3行为真。 |
只有在 p、q 只有一真的情况下, p ⊙ q (p 不相容析取 q)才为真。
先设定复合命题 p ⊙ q 为真,则(为真的) p ⊙ q 对应第2、3行,
那么其负命题 ﹁(p ⊙ q)则对应 第1、4行,
观察这两行可知, p ⊙ q 为假时,有两种情况,
即 p、q 同真;或者 p、q 同假。
因此,可以将这两行的情况 归纳为 一个选言命题。
同样的,设定命题p、q为真,则 p、q 为假就写为 ﹁p、 ﹁q。
第1行写为 p ∧ q ,第4行写为 ﹁p ∧ ﹁q,组合为: (p ∧ q) ∨ (﹁p ∧ ﹁q)
所以,复合命题 p ⊙ q 的负命题的等值关系式写为:
﹁(p ⊙ q) ↔ (p ∧ q) ∨ (﹁p ∧ ﹁q)
充分条件假言命题的负命题的等值式
充分条件假言命题真值表
| p | q | p → q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 先设定复合命题 p → q 为真,则(为真的) p ∧ q 对应第1、3、4行, |
那么其负命题 ﹁(p → q)则对应 第2行,
观察这一行可知, p → q 为假时,只有一种情况,即 前件 p 为真,而后件 q 为假。
因此,可以将这一行的情况 归纳为 一个联言命题。
同样的,设定命题p、q为真,则 q 为假就写为 ﹁q。
所以,复合命题 p → q 的负命题就写为:
p ∧ ﹁q
等值关系式写为:
﹁(p → q) ↔ (p ∧ ﹁q)
必要条件假言命题的负命题的等值式
必要条件假言命题真值表
| p | q | p ← q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 必要条件假言命题的真值表(逻辑性质)为 3行真,1行假,(不算标题)第3行 为假。 |
先设定复合命题 p ← q 为真,则(为真的) p ← q 对应第1、2、4行,
那么其负命题 ﹁(p ← q)则对应 第3行,
观察这一行可知, p ← q 为假时,只有一种情况,即 前件 p 为假,而后件 q 为真。
因此,可以将这一行的情况 归纳为 一个联言命题。
同样的,设定命题p、q为真,则 p 为假就写为 ﹁p。
所以,复合命题 p ← q 的负命题就写为:
﹁p ∧ q
等值关系式写为:
﹁(p ← q) ↔ (﹁p ∧ q)
充分必要条件假言命题的负命题的等值式
充分必要条件假言命题真值表
| p | q | p ↔ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 充分必要条件假言命题的真值表(逻辑性质)为 2行真,2行假,(不算标题)第2、3行(中间两行) 为假。 |
先设定复合命题 p ↔ q 为真,则(为真的) p ← q 对应第1、4行,
那么其负命题 ﹁(p ↔ q)则对应 第2、3行,
观察这两行可知, p ↔ q 为假时,有两种情况,一为 前件真,后件假, 一为 前件假,后件真。
或者是第一种情况,或者是第二种情况。
因此,可以将这两行的情况 归纳为 一个选言命题。
同样的,设定命题p、q为真,则 p、q 为假就写为 ﹁p、﹁q。
第2行写为 p ∧ ﹁q ,第3行写为 ﹁p ∧ q,组合为:
(p ∧ ﹁q) ∨ (﹁p ∧ q)
所以,复合命题 p ↔ q 的负命题的等值关系式写为:
﹁(p ↔ q) ↔ (p ∧ ﹁q) ∨ (﹁p ∧ q)
小结
各 复合命题的负命题的等值式,都可以通过观察真值表得出。
即 观察真值表中 此复合命题 为假 的行。
如果只有1行,则 p、q 的组合 是固定的,p是某值,同时q是某值,
这样就只能写为一个 联言命题。
相容选言命题、充分条件假言命题、必要条件假言命题 这3类 复合命题的负命题都是如此。
如果有2行或以上,p、q 的组合 就不是固定的,p是某值时,q的值可以有两种可能,或者反过来。
这样就要写成一个 选言命题,把 为假的各行,用“或者”连起来。
联言命题、不相容选言命题、充分必要条件假言命题 这3类复合命题的负命题属于这种情况。
不相容选言命题、充分必要条件假言命题 的负命题的写法, 是直接把为假的每一行写成一个复合命题,再“串”起来。 其支命题就是 一行的逻辑表达式。稍长,但很容易理解。
联言命题 的负命题的写法,则做了“归纳”,是以 p、q的负命题作为 选言支。简洁,但有时可能需要再理解一下。
复合命题之间的等值转换
充分条件假言命题 与 必要条件假言命题
从真值表来看,如果两个逻辑表达式的真值表一模一样,那么它们是等值的。
所谓一模一样,是说 支命题 的取值排列一样、对应的逻辑表达式的真假也一样。 例如: p真q假时,p→q为假,q←p也为假
例如,先将充分条件假言命题真值表
| p | q | p → q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
的 p、q 对调:
| q | p | p → q |
|---|---|---|
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 0 | 1 |
即 改为 以 q 为前件,p 为后件
然后,调整各行的顺序, 使 q 列 的值为 1100,p 列的值为1010:
| q | p | p → q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| (这里只需要把原来的第2、3行 位置对调) |
对比必要条件假言命题真值表:
(为避免代码看起来混乱,改用 前件、后件)
| 前件 | 后件 | 前件 ← 后件 | |
|---|---|---|---|
| 1 | 1 | 1 | |
| 1 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 0 | 1 | |
真值部分一模一样。
因此,在改 q 为前件、p为后件 之后, q 与 p 的条件制约关系就是 q 逆蕴涵 p,
即 q ← p
所以,p → q 等值于 q ← p。
p 是 q 的充分条件,则 q 是 p 的必要条件。反之亦然。
只有年满18岁,才有选举权。
如果有选举权,那么一定年满18岁。
只有考前认真复习了,考试才会通过。
如果考试通过了,那么考前一定认真复习了。
假言命题 与 选言命题
假言命题 转 选言命题,与 上述假言命题的负命题 转 选言命题 的方法是一样的。
也可以通过观察真值表 再归纳的方式来进行。
另外,也可以直接把 假言命题的负命题 加上否定,再转一次。
充分条件假言命题
充分条件假言命题 的负命题 和 等值式为: ﹁(p → q) ↔ (p ∧ ﹁q)
那么 充分条件假言命题 本身的 选言命题形式的等值式可以是:
﹁(p ∧ ﹁q) ↔ ﹁p ∨ q
可以记为,开括号,把 “负数” 乘上括号中的 命题代号,并 “颠倒” 联结项符号。
所以:
(p → q) ↔ ﹁p ∨ q
如果要用真值表,可以用以下步骤来整理:
先在 充分条件假言命题真值表中加一列 ﹁p,并根据p的值,写出 ﹁p 的值,
即:
| p | ﹁p | q | p → q |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
然后去掉 p 列,以 ﹁p 为前件,q为后件,按通用顺序(1100、1010)重新排序:
| ﹁p | q | p → q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
(也就是把原来的1、2列,挪到3、4列的下方)
与相容选言命题真值表的真值部分一模一样:
| 前件 | 后件 | 前件 ∨ 后件 |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3行真,1行假,(不算标题)第4行为假。
所以:
p → q 等值于 ﹁p ∨ q
必要条件假言命题
同上,把 必要条件假言命题的负命题的 等值式(﹁p ∧ q)再否定一次:
﹁(﹁p ∧ q) ↔ p ∨ ﹁q
所以:
(p ← q) ↔ p ∨ ﹁q
选言命题
(需要联系到 推理部分) 相容 或 不相容选言命题都可以使用 “否定肯定”式。
如果只有 两个选言支 p、q,那么否定一个,必然肯定另一个。(反过来不一定)
由此推理, 可以得出 选言命题 到 假言命题的 等值式:
p ∨ q ↔ (﹁p → q) ↔ (﹁q → p)
习题
补充
1、确定简单命题的真假 是 确定复合命题 真假 的 必要前提
各简单命题(支命题 本身 或 继续拆分到这一层)是真是假,需要先确定,
然后才能 确定 复合命题的 真假。
可以有个 总→分→总 的过程。
第一个“总” 是找联结词,确定整个命题的类型。
“分” 是 拆出 支命题,确定其 真假。
第二个“总”是根据 支命题的真假,再加上 联结词,“算”出 整个复合命题的真假。
以上是说 命题, 在推理中,复合命题推理,有一部分形式,也一样需要 先定 复合命题的真假。
2、要引入 表达 和 接收 两个不同角度 来 区分,以帮助理解对复合命题的定义
表达者 要表达的,是其所认为的真命题。这可以看作一个基本设定。
即 说话人 总是以为 这个命题是真的,才把它表达出来。
原命题、否命题、逆命题、逆否命题
(属 复合命题)
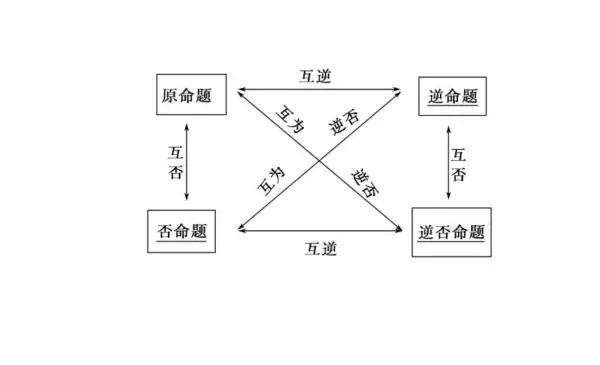
四种命题具有形式:设p为原命题条件,q为原命题结论则:
(1)原命题:若p则q ;
充分条件命题
(2)逆命题:若q则p ;
前件、后件 对调
(3)否命题:若非p则非q;
否定前件,则否定后件。必要条件命题
(4)逆否命题:若非q则非p。
即 逆命题 的 否命题。
原命题,逆否命题同真同假;
否命题,逆命题同真同假
说明:以上的写法,都是从 以 p 、q (而不是 非p、非q)作为“素材” 的角度来说的。