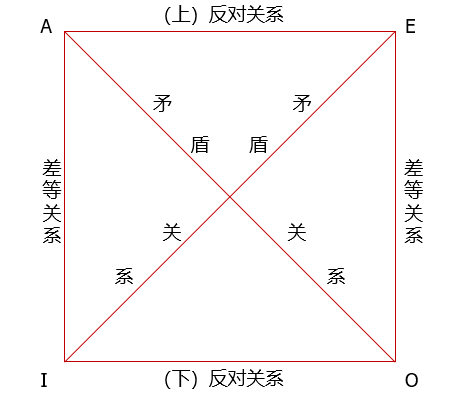
同素材的直言命题间的真假(制约)关系,称为 对当关系。(逻辑方阵、对当方阵)
所谓“真假关系”,是说 在A、E、I、O四个命题中,当已知某个命题为真或假时,可推另两个或三个命题的真或假。
不是都能推出。有的只能推出2个。
具体有四类关系:
- (上)反对关系
- 下反对关系
- 矛盾关系
- 差等关系(从属关系)
两两成对
| 关系 | 真假(制约)关系 | 具体真假情况 |
|---|---|---|
| (上)反对关系 | 可以同假,不能同真 | 一真一假,或 两个都假 |
| 下反对关系 | 可以同真,不能同假 | 一真一假,或 两个都真 |
| 矛盾关系 | 只能一真一假,不能同真,也不能同假 | 一真一假。 |
| 差等关系 | (上下参照图片) 真,从上往下看,上真则下真; 假,从下往上看,下假则上假。 | SAP真,则SIP真。 SEP真,则SOP真。 SIP假,则SAP假。 SOP假,则SEP假。 |
SaP、SeP 是矛盾关系,只能一真一假。
补充说明
理解 A与O、E与I的矛盾关系,可以从 周延性 的角度 来看 (还有命题变换的角度)
SIP的S 是不周延的,“有些” 只是“某一个”部分 但是如果 SIP 为假, 那么,要使 SIP 为假,是不是需要 “每一个”部分的(S) 都不是 P ? 任意一个部分的S 都不是P 这样 SIP 才能为假,
任意一个部分的S 都不是P,即 全部的 S 都不是P (这时S变成周延的了) 即 SEP 为真。
同理,SOP的S也是不周延的,但是如果要 使 SOP 为假, 则需要 “每一个”部分的(S) 都是P → SAP
开会时,主持会议的人(以为没到齐)说:
- 有人没来。
旁人更正说:
- (不,)都来了。
只要有任何一个人没到,“有人没来” 都是 真的。
要使 “有人没来” 为假,则 需 任何一个人 都要到,即 “所有人都来”。
所以, SOP 为假,SAP 必为真。
练习
根据命题的对当关系,由已知下列命题的真假,断定同素材的其他三种命题的真假
1.已知“某单位职工都买了电冰箱”为假。
2.已知“某班同学都不是会打桥牌的”为真。
3.已知“有的科学家是自学成才的”为真。
4.已知“有的教授不是懂外语的”为假。
说明:先确定当前命题的 类型 (A、E、I、O),然后 说 出 其它 三个命题,并推出其 真假情况。
以下是关于某中学甲班同学参加夏令营的三个断定:
(1)甲班有学生参加了夏令营。
(2)甲班所有学生都没有参加夏令营。
(3)甲班的蔡明没有参加夏令营。
如果这三个断定中只有一项为真,则以下哪项一定为真?
A.甲班同学并非都参加了夏令营。
B.甲班同学并非都没有参加夏令营。
C.甲班参加夏令营的学生超过半数。
D.甲班仅蔡明没有参加夏令营。
E.甲班仅蔡明参加了夏令营。
提示:上题分两步来解。
- 确定 (1)、(2)、(3)中 哪一项为真。
- 由 1 的 结论 分析 A~E 的 真假,找出 必真 的一项。
1 具体一些, 是 根据 AEIO命题的 对当关系,加上已知条件“只有一项为真” 来 推理。
再具体一些,可先 写出 (1)、(2)、(3) 的命题类型, 然后 画出 对当关系图,
从假设 某项 真 ( 例如 (1)) 开始推理。 可以列表 推理。