同一律
A是A
A→A,A ↔ A
以概念为例,
在同一段话(同一篇文章、同一本书……)中多次出现时,A 始终是 A,不能中途更改了概念(内涵、外延都变了,只是字面上还是同一个词语)却还继续当同一个概念使用。
也不能中途“混入” 字面相同的另一个概念,当成A来使用。
更换词语的情况是容易识别的,字面相同但却是不同概念的情况需要注意。
例如:同形异义词、同一个词既能表达 集合概念 又能表达 非集合概念等。
矛盾律
又称 不矛盾律
A不是非A
﹁(A ∧ ﹁A)
并非(A并且非A), A 与 非A 同真是不可能的。
不能在说 A是真的 的同时,又说 A是假的。 两个说法之一必假。
不能既肯定A(说A是真的),又否定A(说 非A是真的,即说A也是假的)
A 是真的,非A就是假的。A 是假的,非A就是真的。
而 真的 不是 假的;假的 不是 真的。
所以,A不是非A。
A 与 非A 不可同真,必有一假。(在此基础上,也自然必有一真)
有些书上的 文字表述 与 逻辑表达式 并不完全一致。
并且文字表述本身仍有不严密之处。
文字表述是 “矛盾关系 或 反对关系”,但 逻辑表达式“A 或 非A” 只能是矛盾关系。不管A是概念(则A 与 非A 的外延是 矛盾关系),还是命题(则 A 与 非A 的真值 是 矛盾关系),都是如此。
另外,虽然在概念中,两个概念的外延的反对关系只有一种,但是在命题中,“反对关系” 分为 (上)反对关系 和 下反对关系。那是两者都可呢,还是其中之一呢?
还是应以 逻辑表达式为准,即 矛盾律 所说的 应是 具有矛盾关系的两个思维形式,不能同真,必有一假。
然后由此延伸去理解。
在概念中,在外延互斥这一点上,矛盾关系可以涵盖反对关系。
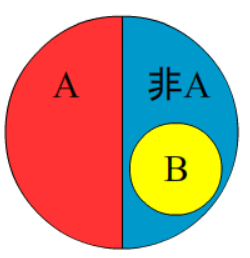
如上图,A 与 非A(或者说 是A 与是 非A),不能同真,必有一假。
同样,A 与 B(或者说 是A 与是 B),也是不能同真的,必有一假。
在命题中,(上)反对关系也是不能同真的,必有一假。这种真假制约关系,也能被 矛盾律涵盖。(矛盾律 能涵盖到 (上)反对关系中的“不能同真,必有一假”,不过“管不了” “可以同假”的情况。)
排中律
A 或 非A
A ∨ ﹁A
如果两个选言支都为假,此选言命题就为假。
反过来,此选言命题为真(规律成立),两个选言支就不能都为假。
不能既否定A(说A是假的),又否定 非A(说 非A也是假的,即说A是真的)。
在 A 与 非A 之中,必须要肯定一个。
这是一个选言命题,如果 两项都为假,则命题为假。 所以,要确保不违反此规律, 就 “不可同假”,必有一真。
参考分析:
从逻辑表达式看,矛盾律 和 排中律 所说是都是矛盾关系(一真一假),是从不同的角度来说的。
矛盾律 从不可同真,必有一假的角度来说。
排中律 从不可同假,必有一真的角度来说。
(上)反对关系,在构成真假制约关系时, 可以应用矛盾律。例如已知一真,则另一个必假。因为不可同真,必有一假。
下反对关系,在构成真假制约关系时, 也可以应用排中律。例如已知一假,则另一个必真。因为不可同假,必有一真。
稍早的书 一般就是以上 三大规律。
三大规律 从不同的角度来 保证 思维的确定性(始终围绕同一个具体的思维形式、真假分明)。
三大规律 要求必须遵守,则 换言之,也可以不遵守,可以违背 (不像自然规律、物理规律,更靠近 法律的“律”) 不过,这个可以 不是 “没问题”的可以,是“后果自负”的可以。
充足理由律
q 真,因为 p 真 且 由 p 能够推出 q 。
可以这样理解:
前提p真,并且p能合乎逻辑地推出q。
这样 q 才是真的。
然后把这个过程“倒叙”一下:
q真,因为 p 真 且 由 p 能够推出 q 。
充足理由律 要求 前提真 且推理形式有效,才能推出结论。
要求在论证中,论题的论据必须充分、推理形式必须有效。